НовоВики. «Мой Новосибирск родной!»
Участник:Группа №1 — различия между версиями
(→Свойства квадрата) |
(→Свойства квадрата) |
||
| Строка 62: | Строка 62: | ||
Площадь квадрата больше площади любого прямоугольника с тем же периметром. | Площадь квадрата больше площади любого прямоугольника с тем же периметром. | ||
В своей книге «Удивительный квадрат» Б.А. Кордемский и Н.В. Русалев подробно описывают доказательства этих свойств. | В своей книге «Удивительный квадрат» Б.А. Кордемский и Н.В. Русалев подробно описывают доказательства этих свойств. | ||
| − | [[Файл:1-1-.jpg ]] | + | |
| + | [[Файл:1-1-.jpg ]] | ||
| + | |||
| + | |||
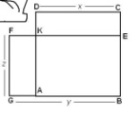
Для доказательства первого свойства был сравнен периметр квадрата АВСD, со стороной x, данной площади (рис.1) с каким-либо прямоугольником ВЕFG,с большей стороной y, той же площади. Очевидно, что y больше x, ; тогда другая сторона z непременно меньше x. По чертежу видно, что АВЕК- общая часть и для квадрата и для прямоугольника; остаются два равновеликих прямоугольника АКFG и КЕСD, т.е. АG•FG = DС•КD. Но так как FG<DC, то AG>KD или y–x > x–z. Отсюда y+z>2x и 2y+2z>4x, то есть периметр любого прямоугольника, равновеликого квадрату, больше периметра квадрата. Значит, среди всех равновеликих прямоугольников квадрат обладает наименьшим периметром. | Для доказательства первого свойства был сравнен периметр квадрата АВСD, со стороной x, данной площади (рис.1) с каким-либо прямоугольником ВЕFG,с большей стороной y, той же площади. Очевидно, что y больше x, ; тогда другая сторона z непременно меньше x. По чертежу видно, что АВЕК- общая часть и для квадрата и для прямоугольника; остаются два равновеликих прямоугольника АКFG и КЕСD, т.е. АG•FG = DС•КD. Но так как FG<DC, то AG>KD или y–x > x–z. Отсюда y+z>2x и 2y+2z>4x, то есть периметр любого прямоугольника, равновеликого квадрату, больше периметра квадрата. Значит, среди всех равновеликих прямоугольников квадрат обладает наименьшим периметром. | ||
Для доказательства второго свойства авторы книги использовали метод, когда доказывают обратные теоремы – от противного. | Для доказательства второго свойства авторы книги использовали метод, когда доказывают обратные теоремы – от противного. | ||
Версия 16:10, 1 ноября 2010
Содержание |
Автор проекта
Группа №1
Что было бы, если не было бы квадрата?
Введение
Присмотритесь-ка к квадрату: Он здоровый, тороватый, Он надежнее как друг, Чем уж слишком круглый круг. В нем четыре стороны И все стороны равны. Честен каждою чертой, Каждый угол в нем прямой. Тем еще квадрат отличен, Что вполне он симметричен, Треугольников всех рать Вам того не может дать. Е. Паин
Правильные многоугольники с глубокой древности считались символом красоты и совершенства. Из всех многоугольников с заданным числом сторон наиболее приятен для глаза правильный многоугольник, у которого равны все стороны и равны все углы. Одним из таких многоугольников является квадрат или другими словами, квадрат- это правильный четырехугольник. Дать определение квадрату можно несколькими способами: квадрат – это прямоугольник, у которого все стороны равны и квадрат – это ромб, у которого все углы прямые. Из школьного курса геометрии известно: 1 у квадрата все стороны равны, 2 все углы прямые, 3 диагонали равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам. 4 Квадрат обладает симметрией, которая придает ему простоту и известное совершенство формы: квадрат служит эталоном при измерении площадей всех фигур. Это малая часть того, что можно раскрыть в этом вопросе, потому что современной математике известно достаточно много интересных и полезных свойств квадрата. Поэтому целью данного реферата является: 1 подробнее исследовать свойства квадрата, 2 рассмотреть геометрические способы раскроя квадрата, 3 обосновать возможности превращений фигур при помощи разрезания квадрата, 4 найти различные варианты построений, которые можно воспроизвести при помощи перегибания квадратного листа бумаги, и выявить преимущества в таком виде построений. При изучении данной темы использовались статьи из книг и журналов, посвященных отдельным вопросам метематики. В. Ф. Каган «О преобразовании многогранников». В этой книге приводится доказательство теоремы Ф. Больаи на примере квадрата. В книге «Удивительный квадрат» Б.А. Кордемского и Н.В. Русалева подробно изложены доказательства некоторых свойств квадрата, приведены пример «совершенного квадрата» и решение одной задачи на разрезание квадрата арабским математиком Х века Абулом Вефой. В книге И. Лемана «Увлекательная математика» собрано несколько десятков задач, среди которых есть и такие, возраст которых исчисляется тысячелетиями. Из этой книги в реферате были использованы задачи на разрезания квадрата. Книги Я.И. Перельмана принадлежат к числу наиболее доступных из книг, посвященных занимательной математике. В книге «Занимательная геометрия» популярно изложен вопрос о фигурах с наибольшей площадью при данном периметре или с наименьшим периметром при данной площади. Для полного представления о построении при помощи перегибания квадратного квадрата листа бумаги была использована книга И.Н. Сергеева «Примени математику».
Цели исследования
- Выяснить,влияет ли одна и таже данная длина границ на площадь фигур заключаемую этой границей
Задачи.
- Изучить историю развития геометрических знаний, связанных с измерением площадей
- Найти известные исторические задачи, касающиеся вопроса, как можно окружить больше земли?
- Сравнить площади четырёхугольников с одинаковым периметром
- Сравнить площади квадрата и треугольника данного периметра Изучить исторические сведения, связанные с измерением площадей.
- Сравнить площади квадрата и круга одинакового периметра
- Сравнить площади квадрата и правильных многоугольников при одной и той же длине границ
- Найти правила игры с квадратом или с его частями
- Сконструировать фигуры различной формы из квадрата или из его частей
- Оформить презентации учащихся.
- Оформить публикации.
- Научиться делать выводы и оформлять результаты исследования.
Гипотеза исследования.
Фигуры с равными периметрами ограничивают равные площади
Свойства квадрата
У квадрата есть два практичных свойства: Периметр квадрата меньше периметра любого равновеликого ему прямоугольника, Площадь квадрата больше площади любого прямоугольника с тем же периметром. В своей книге «Удивительный квадрат» Б.А. Кордемский и Н.В. Русалев подробно описывают доказательства этих свойств.
Для доказательства первого свойства был сравнен периметр квадрата АВСD, со стороной x, данной площади (рис.1) с каким-либо прямоугольником ВЕFG,с большей стороной y, той же площади. Очевидно, что y больше x, ; тогда другая сторона z непременно меньше x. По чертежу видно, что АВЕК- общая часть и для квадрата и для прямоугольника; остаются два равновеликих прямоугольника АКFG и КЕСD, т.е. АG•FG = DС•КD. Но так как FG<DC, то AG>KD или y–x > x–z. Отсюда y+z>2x и 2y+2z>4x, то есть периметр любого прямоугольника, равновеликого квадрату, больше периметра квадрата. Значит, среди всех равновеликих прямоугольников квадрат обладает наименьшим периметром.
Для доказательства второго свойства авторы книги использовали метод, когда доказывают обратные теоремы – от противного.
Дан квадрат, периметр которого равен p, а площадь равна q.Пусть существует прямоугольник, периметр которого тоже равен p, а площадь Q>q. Затем авторы построили новый квадрат, равновеликий этому прямоугольнику, то есть с площадью, тоже равной Q, и, следовательно, большей, чем площадь данного квадрата. Но по предыдущей теореме периметр нового квадрата p <p.Значит, площадь нового квадрата больше площади данного, а периметр меньше. Это невозможно. Следовательно, не существует прямоугольника с периметром таким же, как у квадрата и площадью большей, чем площадь квадрата. Не существует также и прямоугольника, имеющего площадь, равную площади данного квадрата, так как в этом случае периметр квадрата меньше периметра прямоугольника, что противоречит условию.
Эти свойства можно считать практичными, потому что их можно использовать в жизненных ситуациях. Например, если нужно огородить изгородью, забором или решёткой участок земли определённой площади так, чтобы длина ограды была насколько возможно малой, причём огороженный участок должен быть прямоугольной формы, но с любым соотношением сторон. В переводе на точный, математический язык это значит: какой из прямоугольников данной площади имеет наименьший периметр?
В книге «Занимательная геометрия» Я.И. Перельмана приведены примеры и популярно изложены вопросы о фигурах с наибольшей площадью при данном периметре или с наименьшим периметре при данной площади
Выводы
- Свойства квадрата находят применение в различных областях жизни.
- Знание геометрии меняет жизнь людей к лучшему.
Источники информации
- Геометрия 7-9. Учебник для общеобразоват. учреждений/ Л. С. Атанасян, В. Ф. Бутусов,С. Б. Кадомцев, Э. Г. Позняк, И. И. Юдина - М.,Просвещение,2002. – 335 с.
- Задачи по планиметрии с практическим содержанием / С. С. Варданян - М.,Просвещение, 1999– 144 с.
- Факультативный курс по математике: Учебное пособие для 7 - 9 классов средней школы / Сост. И. Л. Никольская. - М., Просвещение. 1991– 328 с.
- Энциклопедический словарь юного математика /Сост.А. П. Савин. - Педагогика, 1985 – 463 с.
- Б.А. Кордемский, Н.В. Русалев «Удивительный квадрат». Москва-Ленинград, 1952 г.
- В.Ф. Каган «О преобразовании многогранников». Гостехиздат, 1933 г.
- Г. Штейнгауз «Математический калейдоскоп». Гостехиздат, 1949 г.
- Е.И. Игнатьев « В царстве смекалки». Москва «Наука», 1981 г.
- З.А. Михайлова «Игровые занимательные задачи для дошкольников». Москва «Просвещение», 1990 г.
- И. Леман «Увлекательная математика». Москва «Наука» 1978 г.
- И.Н. Сергеев «Примени математику». Москва «Наука», 1989 г.
- «Квант» 1989. №5 – С. 40.
- Р. Хонсбергер «Математические изюминки». Москва «Наука», 1992 г.
- Я.И. Перельман «Живая математика». Москва «Наука», 1977 г.
- Я.И Перельман «Занимательная геометрия». Москва «АСТ», 2003 г.